目标检测任务:是找出图像中所有感兴趣的而目标(物体),确定他们的位置和大小,是机器视觉领域的核心问题之一。
目标检测算法的工作流程
两阶段方法
两阶段目标检测算法以R-CNN系列为代表的一系列方法。它们的工作流程是,给定一幅图像,首先从图像中获取候选框,然后对候选框进行分类和位置修正。
单阶段方法
单阶段目标检测算法以YOLO和SDD为代表。
Anchor Free方法
Anchor Free目标检测算法以FCOS,CenterNet为代表。
RPN的原理
RPN第一次出现在世人眼中是在Faster RCNN这个结构中,专门用来提取候选框,在RCNN和Fast RCNN等物体检测架构中,用来提取候选框的方法通常是Selective Search,是比较传统的方法,而且比较耗时,在CPU上要2s一张图。所以作者提出RPN,专门用来提取候选框,一方面RPN耗时少,另一方面RPN可以很容易结合到Fast RCNN中,称为一个整体。RPN的引入,可以说是真正意义上把物体检测整个流程融入到一个神经网络中。
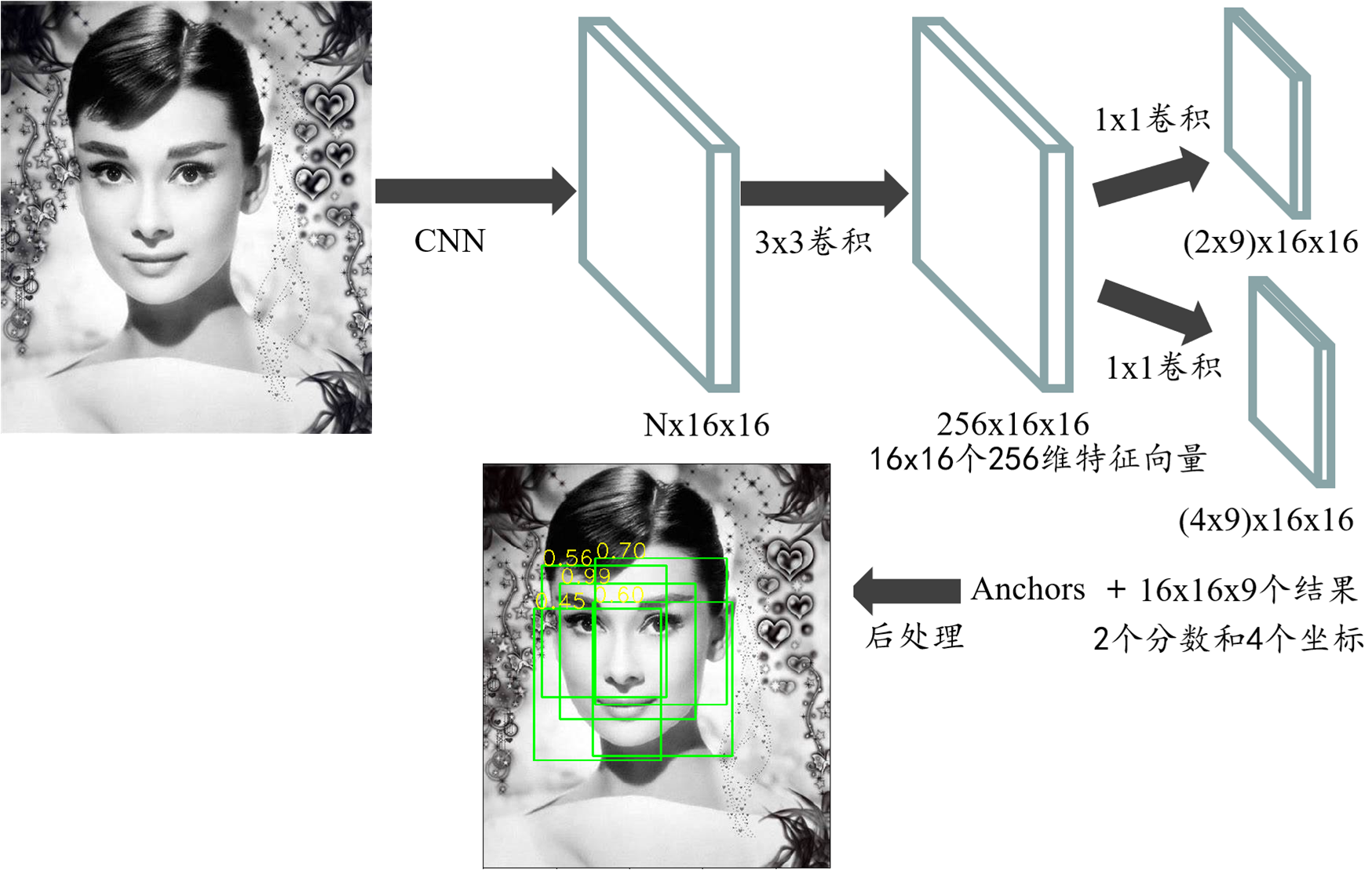
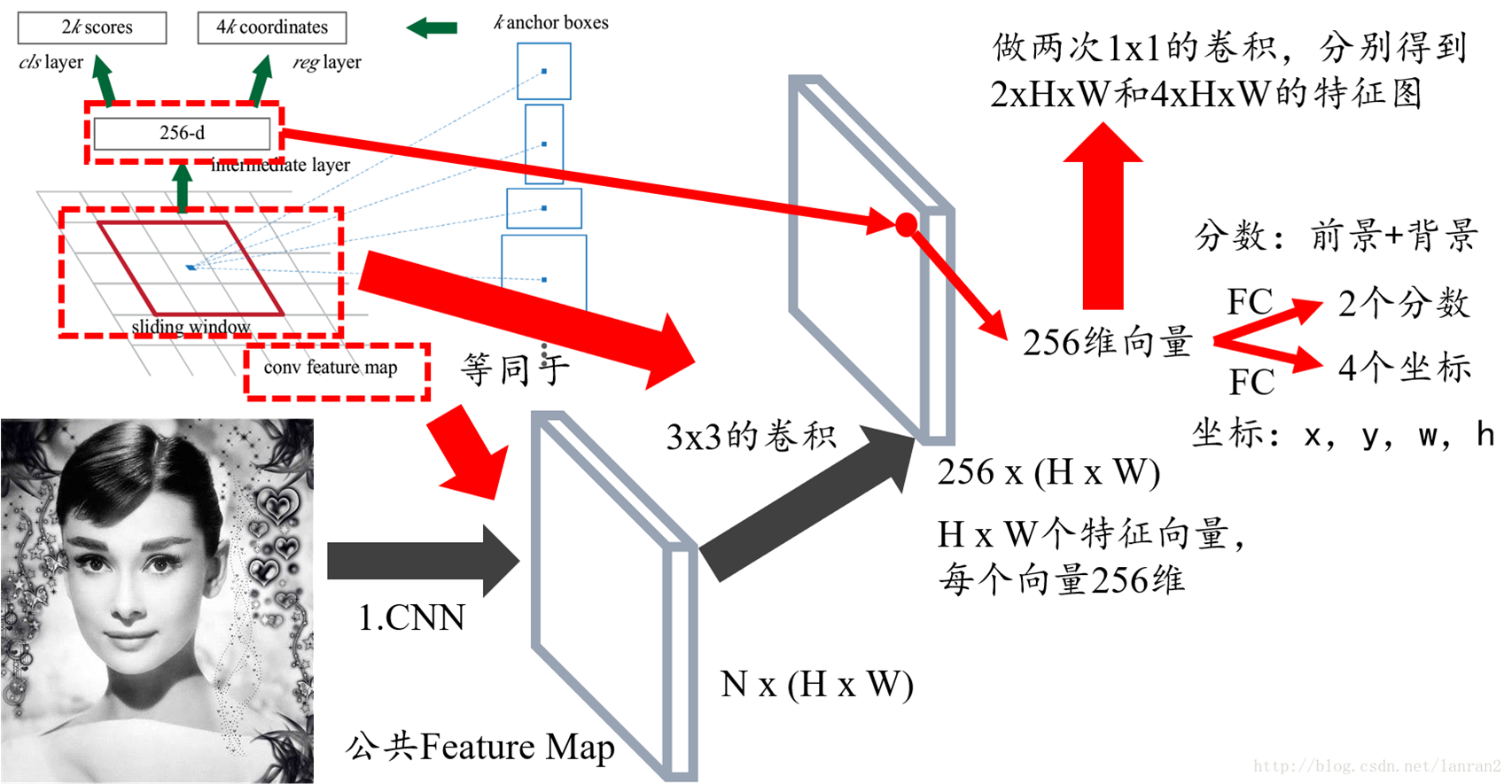
RPN 运作机制
首先通过一系列卷积得到公共特征图,假设他的大小是$N \times 16 \times 16$,然后我们进入RPN阶段,首先经过一个$3 \times 3$的卷积,得到一个$256 \times 16 \times 16$的特征图,也可以看作$16 \times 16$个256维特征向量,然后经过两次$1 \times 1$的卷积,分别得到一个$18 \times 16 \times 16$的特征图,和一个$36 \times 16 \times 16$的特征图,也就是$16 \times 16 \times 9$个结果,每个结果包含2个分数和4个坐标,再结合预先定义的Anchors,经过后处理,就得到候选框。
RoIPooling、RoIAlign和RRoIPooling
从feature map上经过RPN得到一系列的proposals,大概2k个,这些bbox大小不等,如何将这些bbox的特征进行统一表示就变成了一个问题。即需要找一个办法从大小不等的框中提取特征使输出结果是等长的。
RoIPooling
根据输入的图像,将RoI映射到feature map对应位置上,然后将映射后的区域划分为固定数量的块(bin),然后在每一个块(bin)中做maxpooling,举例如下图
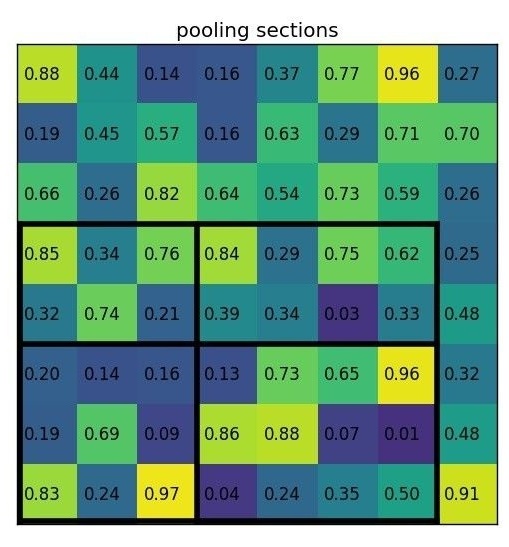
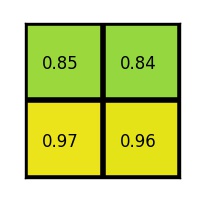
缺点:ROI Pooling 需要取整,这样的取整操作进行了两次,一次是得到bbox在feature map上映射时,一次是对映射后的区域划分同等大小的块(bin)时。这样两次取整操作,会对后面的回归定位产生影响,尤其是小目标。
ROIAlign
将bbox区域按输出要求的size进行等分,很可能等分后各顶点落不到真实的像素点上;在每个bin中再取固定的4个点(作者实验后发现取4效果较好),也就是图二右侧的蓝色点;针对每一个蓝点,距离它最近的4个真实像素点的值加权(双线性插值),求得这个蓝点的值;一个bin内会算出4个新值,在这些新值中取max,作为这个bin的输出值;最后就能得到$2\times 2$的输出。
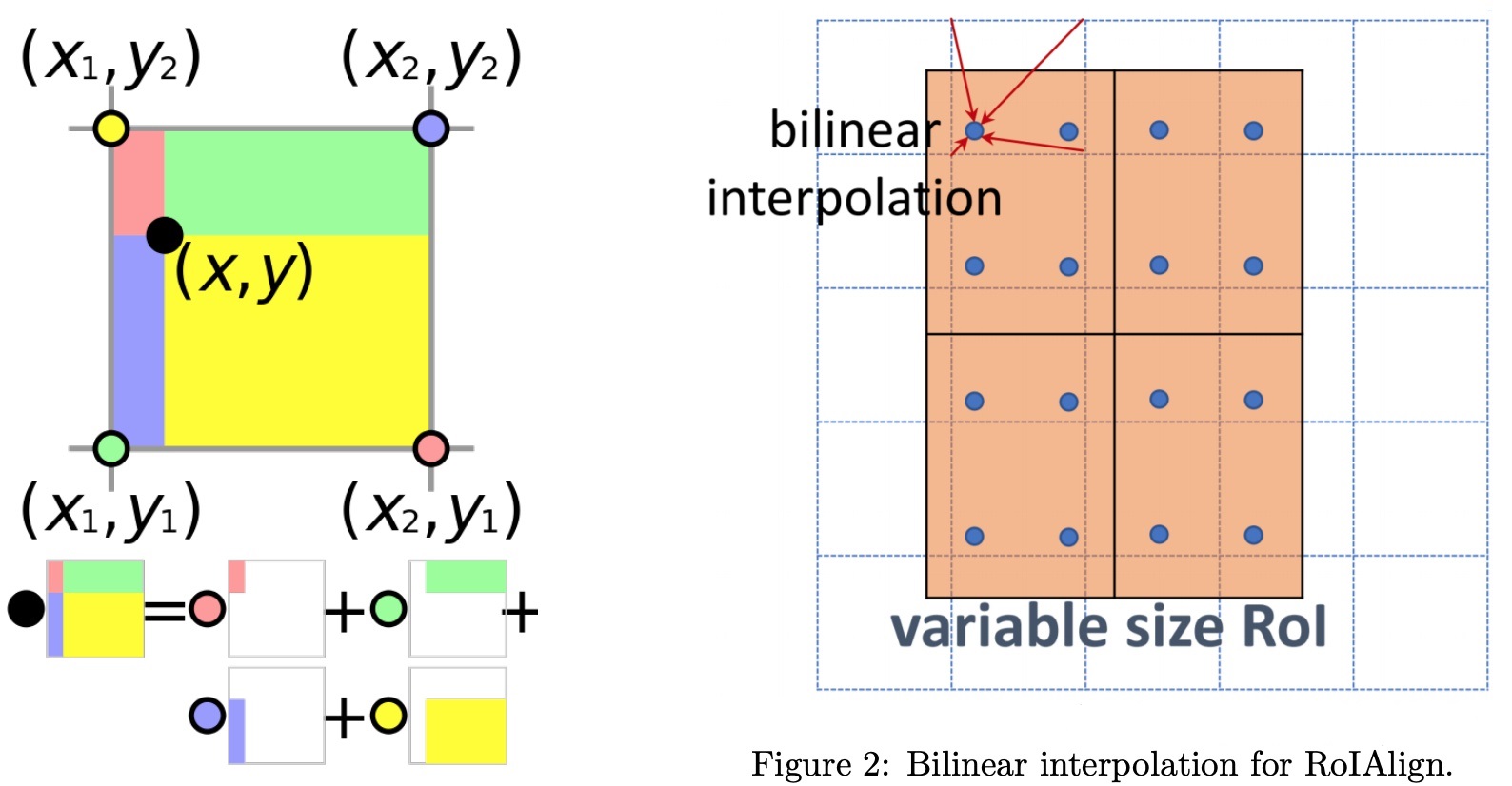
RRoIPooling
RPN得到的候选区域是旋转矩形,而传统的RoI池化只能处理与坐标轴平行的候选区域,因此作者提出了RRoI Pooling用于RRPN中的旋转矩形的池化。首先需要设置超参数 $H_r$ 和 $W_r$,W,H分别表示池化后得到的Feature Map的高和宽。然后将RRPN得到的候选区域等分成 $H_r \times W_r$ 个小区域,每个子区域的大小是$(\frac{W}{W_r}) \times ( \frac{H}{H_r}$。这时每个区域仍然是带角度的,如图所示。接着通过仿射变换将子区域转换成平行于坐标轴的矩形,最后通过Max Pooling得到长度固定的特征向量。
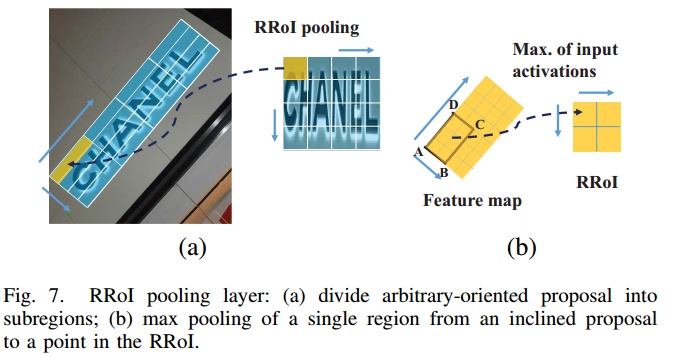
需要对有角度的roi区域仿射变换到与坐标轴对齐的矩形数组中,再采用max pooling得到相同尺寸的特征图。
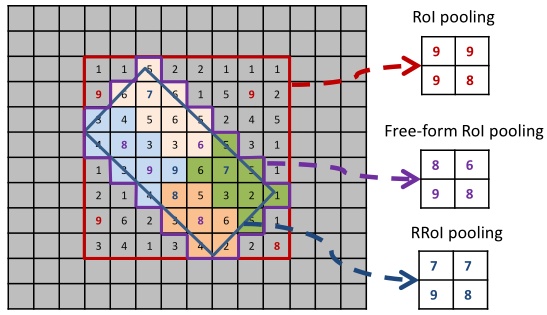
RROI Pooling的计算流程如算法2的伪代码。其中第一层for循环是遍历候选区域的所有子区域,5-7行通过仿射变换将子区域转换成标准矩形,第二个for循环用于取得每个子区域的最大值,10-11行由于对标准矩形中元素的插值,使用了向下取整的方式。

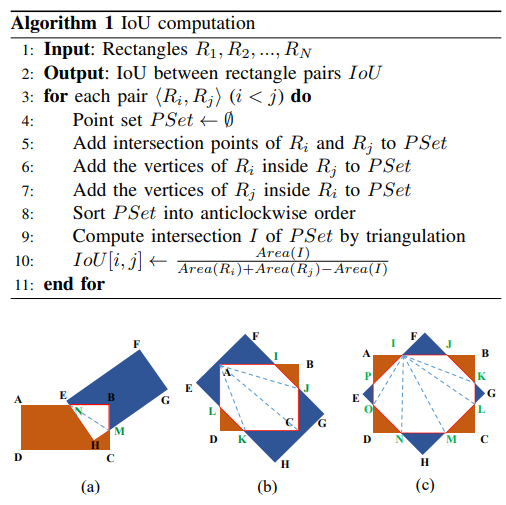
IoU计算
水平框IoU计算
直接看代码!!!
参考代码(Python 版本)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
areas1 = (x1[1]-x1[0]+1)*(y1[1]-y1[0]+1)
areas2 = (x2[1]-x2[0]+1)*(y2[1]-y2[0]+1)
# x1[0] 表示第一个矩形的左上点的横坐标,x1[1] 表示第一个矩形的右下点的横坐标
# y1[0] 表示第一个矩形的左上点的纵坐标,y1[1] 表示第一个矩形的右下点的纵坐标
# x2[0] 表示第二个矩形的左上点的横坐标,x2[1] 表示第二个矩形的右下点的横坐标
# y2[0] 表示第二个矩形的左上点的纵坐标,y2[1] 表示第二个矩形的右下点的纵坐标
xx1 = np.maximum(x1[0], x2[0])
yy1 = np.maximum(y1[0], y2[0])
xx2 = np.minimum(x1[1], x2[1])
yy2 = np.minimum(y1[1], y2[1])
w = np.maximum(0.0, xx2-xx1+1)
h = np.maximum(0.0, yy2-yy1+1)
inter = w * h # 计算交叠部分的面积
overlaps = inter/(areas1 + areas1 - inter) # 计算IoU
旋转框IoU计算
思路:首先计算两个矩形的所有交点,然后将交点集合按照顺时针排序,固定一个结点作为所有三角形的顶点,使用三角形剖分法计算IOU,即依次计算每一个三角形的面积,最后求和即可得到交叠区域的面积。