研究动机（出发点）

传统的基于滑动窗口的目标检测方法和在最新基于锚框的深度学习算法，然而这两种方法都需要对滑动窗口或锚框进行繁杂的配置。文章中作者提出以一个新的视角来检测目标，即将目标检测作为一个高级语义特征检测任务，如检测边缘，角落，斑点等。作者通过卷积操作将行人的检测任务简化为直接预测中心和比例的任务。所提出的检测器扫描整个图像上的特征点，卷积自然适合于该特征点。提出了的方法实现了anchor free。结果显示该算法在准确率和速度上都有显著提高。

提出了检测的一种新的可能性，即行人检测可以通过卷积简化为简单的中心和尺度预测任务，绕过基于锚的检测器的限制并摆脱最近基于关键点配对的检测器的复杂后处理。

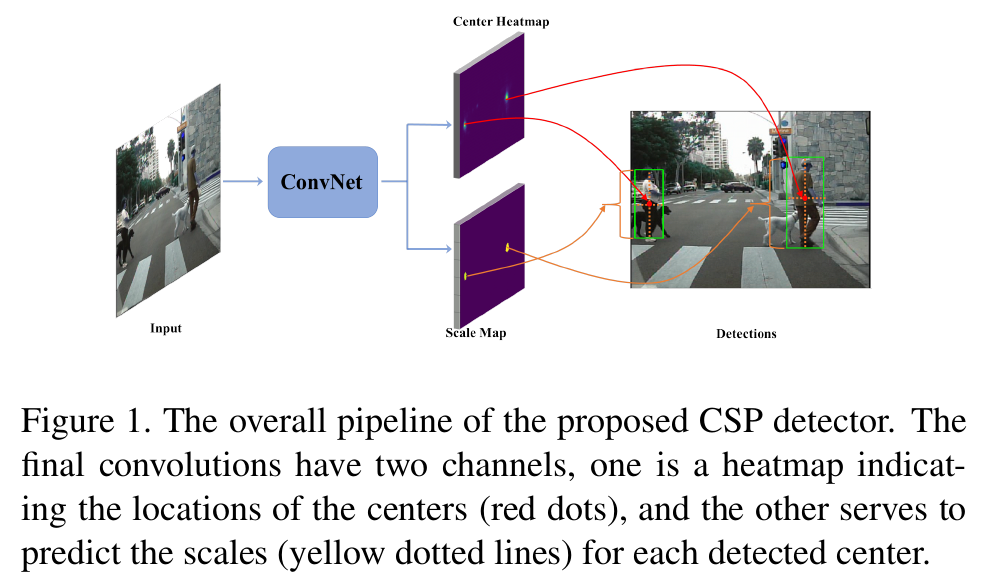
1563007351733

提出的方法（Proposed Method）

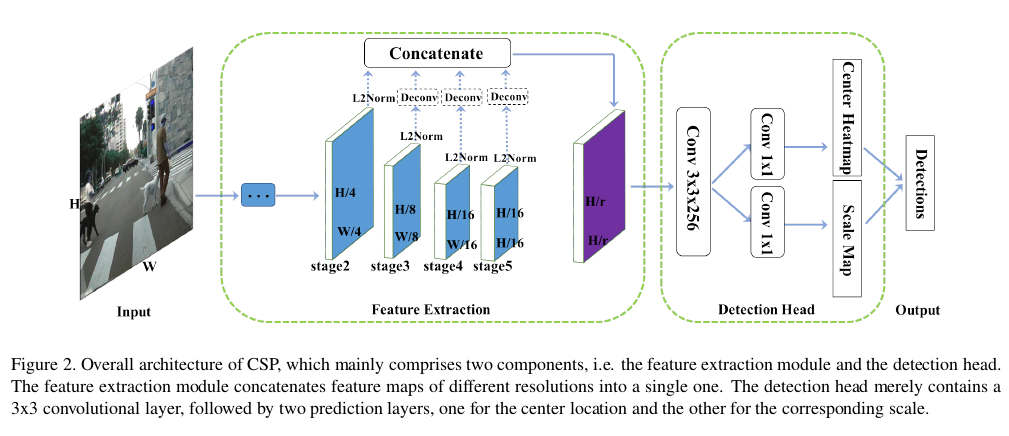
1563008974343

特征提取

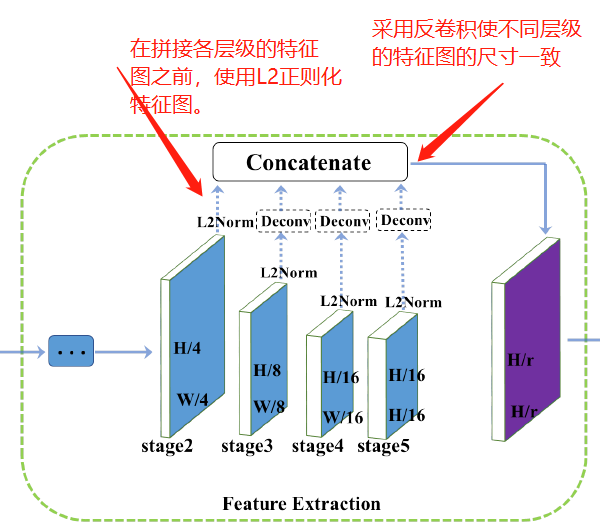
以ResNet50为例，它的卷积层可以分为5个阶段，每个阶段输出的特征图相对于原始输入图像分别下采样2，4，6，8，16，32。在第五阶段采用扩张卷积使其输出是其输入图像尺寸的1/16。较浅的特征图可以提供更精确的定位信息，而较粗略的特征图则包含更多的语义信息，其增加了感受野的尺寸。因此，作者将这些多尺度的特征图进行融合。如下图所示。

1563011335304

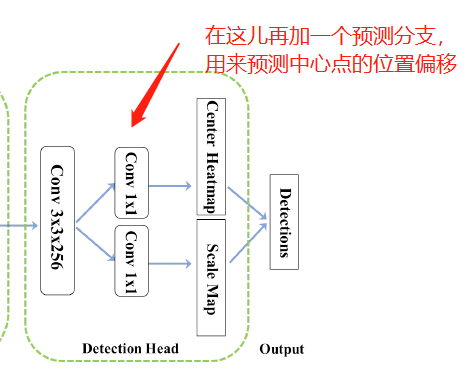
检测头（Detection Head）

在上面特征提取模块中获得的特征图中先使用一个$3\times3$的卷积层将特征图的通道数降为256，然后使用两个并行的$1\times1$的卷积来分别预测中心的heatmap和尺度图(scale map)。

下采样特征图的缺点是定位不精确的问题。为了稍微调整中心位置，可以与上述两个分支并行地附加额外的偏移预测分支。

1563012477100

训练

Ground Truth

给定边界框注释，可以自动生成中心和gt的尺度。如下图所示：

1563017324399

尺度可以定义为长/宽，我们可以预测每个目标的长并通过尺度比率获得目标的宽。对于尺度的 ground truth，第k个正位置(positive location)被赋值为$log(h_{k})$ 对应于第k个目标。为了减少歧义，$log(h_{k})$ 也被赋值给正的半径为2以内的负样本，而其他位置被赋值为零。

当使用预测偏置分支时，中心点偏置的 ground truth 可以被定义为$( \frac{x_k}{r}-\lfloor \frac{x_k}{r}\rfloor, \frac{y_k}{r} -\lfloor \frac{y_k}{r}\rfloor ) $。

损失函数

对于中心预测分支，我们通过交叉损失熵(cross entropy loss)将其表示为分类任务。但是，很难确定”确切“的中心点，因此正负样本难以指定，会给训练带来困难。为了减少围绕正的这些负的的模糊性，作者对每个正的的中心使用一个2D的高斯mask。

\[\begin{array}{l}{M_{i j}=\max _{k=1,2, \ldots, K} G\left(i, j ; x_{k}, y_{k}, \sigma_{w_{k}}, \sigma_{h_{k}}\right)} \\ {G\left(i, j ; x, y, \sigma_{w}, \sigma_{h}\right)=e^{-\left(\frac{(i-x)^{2}}{2 \sigma_{w}^{2}}+\frac{(j-y)^{2}}{2 \sigma_{h}^{2}}\right)}}\end{array}\] \[L_{c e n t e r}=-\frac{1}{K} \sum_{i=1}^{W / r H / r} \alpha_{i j}\left(1-\hat{p}_{i j}\right)^{\gamma} \log \left(\hat{p}_{i j}\right)\] \[\begin{aligned} \hat{p}_{i j} &=\left\{\begin{array}{ll}{p_{i j}} & {\text { if } y_{i j}=1} \\ {1-p_{i j}} & {\text { otherwise }}\end{array}\right.\\ \alpha_{i j} &=\left\{\begin{array}{ll}{1} & {\text { if } y_{i j}=1} \\ {\left(1-M_{i j}\right)^{\beta}} & {\text { otherwise }}\end{array}\right.\end{aligned}\] \[L_{s c a l e}=\frac{1}{K} \sum_{k=1}^{K} \operatorname{Smooth} L 1\left(s_{k}, t_{k}\right)\] \[L=\lambda_{c} L_{c e n t e r}+\lambda_{s} L_{s c a l e}+\lambda_{o} L_{o f f s e t}\]

实验结果

1563020424970

1563020480874

1563020502094

论文笔记：High-Level Semantic Feature Detection：A New Perspective for Pedestrian Detection

CSP